Multi-Layer Neural Network
03 Jan 2019본 포스트에서는 Multi-layer Neural Network를 이용하여 Learned XOR gate를 만들어 볼 것이다. 본 포스트에서는 모델 설계하며 및 Parameter Update Rule을 이론적으로 도출하며, 파이썬 코드 기반의 실습은 다음 포스트에서 다룬다.
이전 포스트 [1, 2]에서 보았듯, And gate 역할을 수행하는 Logistic Regression 모델을 학습하는 것이 가능하다. 그러나 선형구조인 Logistic Regression 모델로는 XOR Gate 같은 비선형적인 문제를 풀 수가 없다. 먼저, XOR Gate의 input(\(x_i\))과 ouput(\(y_i\))을 살펴보자.
| \(i\) | \(x_{i}=(x_{0i}, x_{1i})\) | \(y_{i}\) |
|---|---|---|
| \(0\) | \((0,0)\) | \(0\) |
| \(1\) | \((0,1)\) | \(1\) |
| \(2\) | \((1,0)\) | \(1\) |
| \(3\) | \((1,1)\) | \(0\) |
이 문제를 그래프로 한번 나타내보자.

그림을 보면 알겠지만, 어떤 선분을 그어도 저 O와 X를 구분짓는 것이 불가능하다. 즉, 선분 하나로는 하나 이상의 데이터가 잘못 분류되게된다. 그렇다면 신경망 기반 기법으로는 XOR Gate를 학습할 수 없는 것인가? 물론 아니다.
모델 구조
XOR를 학습하기 위해서는 Hidden Layer가 포함된 신경망 구조가 필요하다. 이를 Multi-Layer Neural Network, 줄여서 MLNN이라고 부른다. MLNN은 Logistic Regression 모델보다 구조적으로 약간 복잡하다. 그러다보니 이전 포스트에서 처럼 모든 컴포넌트들을 전부 그리면 너무 복잡한 그림이되므로, 이제부터는 조금 축약된 도식화 방법을 사용할 것이다. 축약된 도식화 방법 소개를 위해 Logistic Regression Model 예제를 보자.
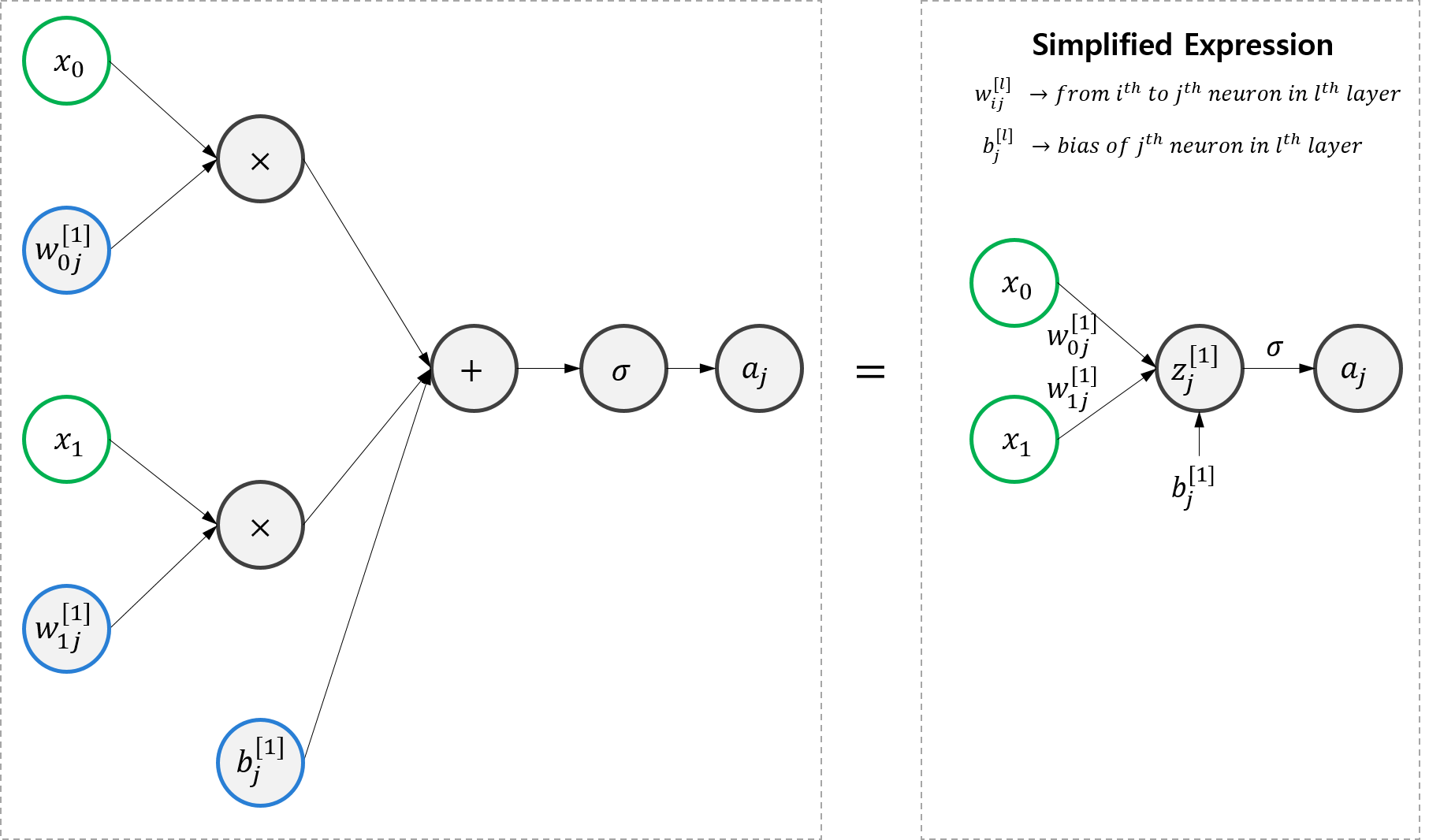
여기서 \(z_{j}^{[l]}\)은 \(l\)번째 layer의 j번째 뉴런으로, 아직 activation function을 거치기 전의 값이다. \(w_{ij}^{[l]}\) 은 \(z_{j}^{[l]}\)를 연산하는 과정에서 필요한 weight으로, (l-1)번째 layer의 i번째 뉴런과 곱해지는 값이다. \(b_{j}^{[l]}\)는 \(z_{j}^{[l]}\)를 연산하는 과정에서 더해지는 bias이다.
간단하게 수식으로 정리하자면,
\[z_{j}^{[l]} = \Sigma_{i} w_{ij}^{[l]}\sigma(z_{i}^{[l-1]}) + b_{j}^{[l]}\]이다.
(단, l=1의 경우 \(z_{j}^{[1]} = \Sigma_{i} w_{ij}^{[1]} x_{i} + b_{j}^{[1]}\) )
이제 간단한 곱연산과 합연산, 활성함수(시그모이드 함수)는 생략해서 표현하고자 한다. 이 표현법을 이용하여 Hidden Layer가 있는 Neural Network를 그려보자.
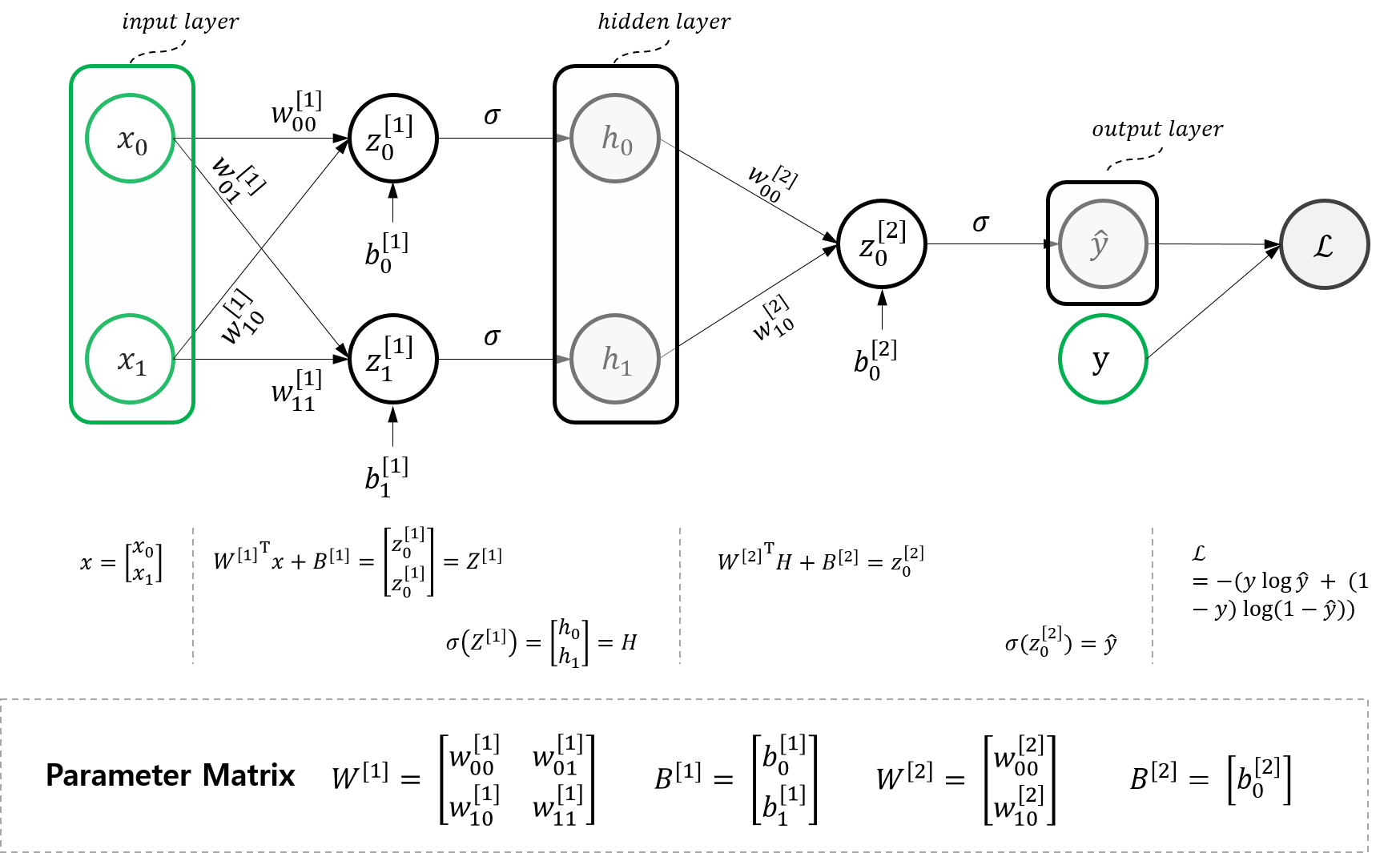
여기서 \(h_1\) 만 보면 이전 포스트의 Logistic Regression 모델과 완전히 같은 구조이다. 망 구조를 분석해보자. 일반적으로 우리는 이 모델을 다음과 같이 세 개의 Layer로 나눈다.
Input Layer: 입력 벡터 레이어 \(x = \begin{bmatrix} x_{0}\\ x_{1} \end{bmatrix}\)Hidden Layer: Input이나 Output과 같이 값을 직접 관찰할 수 있는 값이 아니라는 뜻에서 Hidden Layer라고 부르며, \(H =\begin{bmatrix} h_{0} \\ h_{1} \end{bmatrix}\)output Layer: 출력 벡터 레이어 \(\hat{y}\)
이 신경망 구조를 Logistic Regression 관점으로 볼 수도 있다. 이 신경망 구조에는 총 세개의 Logistic Regression이 존재한다.
Input Layer -> Hidden Layer에서 보이는 두 개의 Logistic Regression (\(h_0\) 과 \(h_1\))Hidden Layer -> Output Layer에서 보이는 하나의 Logistic Regression (\(\hat{y}\))
행렬 연산으로 표현하는 MLNN for learning XOR gate
위 모델을 수식으로 표현해보자.
1. Input Layer
먼저 인풋 레이어인 데이터부터 표현해보자. 각각의 \(x\)는 다음과 같은 열벡터로 표현된다.
\[x = \begin{bmatrix} x_{0} \\ x_{1} \end{bmatrix}\]2. Hidden Layer
\(w_{ij}^{[1]}\) 은 \(z_{j}^{[1]}\)를 연산하는 과정에서 필요한 weight으로, $x_i$와 곱해지는 값이다. \(b_{j}^{[1]}\)는 \(z_{j}^{[1]}\)를 연산하는 과정에서 더해지는 bias이다.
간단하게 수식으로 정리하자면,
\[z_{j}^{[l]} = \Sigma_{i} w_{ij}^{[l]}x_{i} + b_{j}^{[l]}\]이를 행렬 곱으로 정리해보자. \(W^{[1]}\)을 다음과 같이 정의해보자.
\[W^{[1]}= \begin{bmatrix} w_{00}^{[1]} & w_{10}^{[1]} \\ w_{01}^{[1]} & w_{11}^{[1]} \end{bmatrix}\]또, \(B^{[1]}\)를 다음과 같이 정의해보자.
\[B^{[1]}=\begin{bmatrix} b_{0}^{[1]} \\ b_{1}^{[1]} \end{bmatrix}\]이제 \(W^{[1]}, B^{[1]}, x\)를 이용하여 Hidden Layer 유닛 \(h\)는 다음과 같이 표현해보자.
\[\begin{aligned} h = \begin{bmatrix} h_{0} \\ h_{1} \end{bmatrix} &= \sigma(Z^{[1]}) \\ &= \sigma({W^{[1]}}^{T}x+ B^{[1]}) \end{aligned}\]단, 여기서 \(\sigma(A)\)함수는 element-wise 함수로, \(A\)의 각 element에 모두 시그모이드 연산을 취해주는 연산자이다.
2.1 (Optional) 자세한 식 전개
\(h\)를 유도하는 과정을 자세하게 전개해보면 위 구조를 확실하게 이해할 수 있음!
3. Output Layer
이제 Hidden Layer \(H=\begin{bmatrix} h_{0} \\ h_{1} \end{bmatrix}\)와 \(W^{[2]}= \begin{bmatrix} w^{[2]}_{00} \\ w^{[2]}_{10} \end{bmatrix}, B^{[2]}=\begin{bmatrix} b^{[2]}_{0}\end{bmatrix}\) 를 가지고 최종 아웃풋 \(\hat{y}\)을 산출해보자.
\[\begin{aligned} \hat{y} &= \sigma(Z^{[2]}) \\ &=\sigma({W^{[2]}}^{T}H+B^{[2]}) \end{aligned}\]Gradient Descent를 위한 변수별 편미분
이 모델의 예측의 Loss function은 AND gate를 다룬 포스트에서의 Loss function과 같다. 그렇다면 이제 Gradient Descent를 이용하여 Loss function을 최소화하는 Parameter Configuration을 찾아보자.
그러려면 편미분이 필요하다. 우리의 목적은
\[\frac{\partial \mathcal{L}}{\partial W^{[1]}}, \frac{\partial \mathcal{L}}{\partial B^{[1]}}, \frac{\partial \mathcal{L}}{\partial W^{[2]}}, \frac{\partial \mathcal{L}}{\partial B^{[2]}}\]를 구해서 이를 기반으로 Gradient Descent를 함으로써 파라미터를 튜닝하는 것이다.
먼저 \(\frac{\partial \mathcal{L}}{\partial W^{[2]}}, \frac{\partial \mathcal{L}}{\partial B^{[2]}}\)를 구해보자.
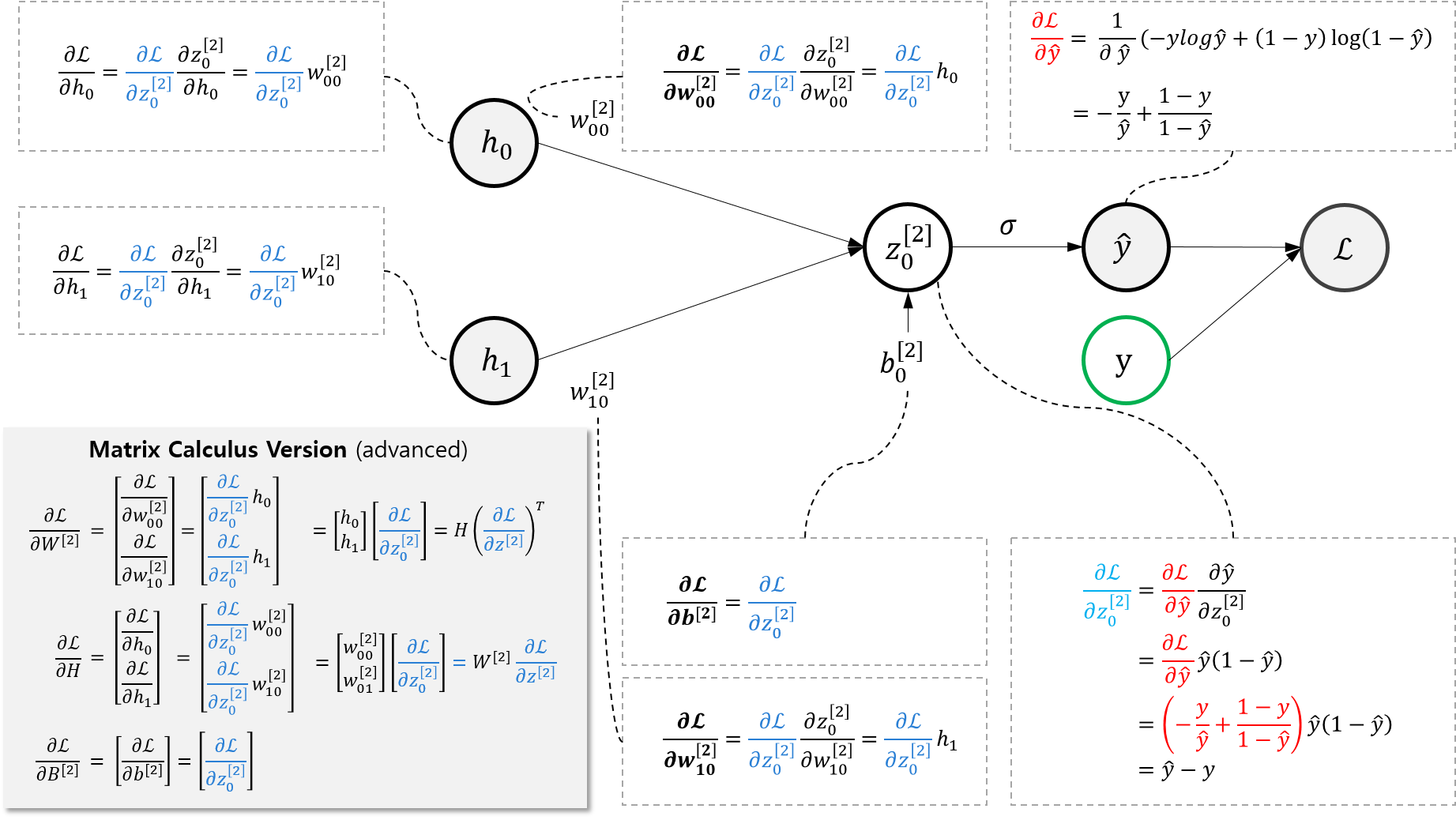
위 그림에서 알 수 있듯,
\[\begin{aligned} \frac{\partial \mathcal{L}}{\partial W^{[2]}}&=H(\frac{\partial \mathcal{L}}{\partial z^{[2]}})^{T}=H(\hat{y}-y)^{T} \\ \frac{\partial \mathcal{L}}{\partial B^{[2]}}&=(\hat{y}-y)\end{aligned}\]이다. 당장은 필요하지 않지만 backpropagation에서 필요한 term을 하나만 더 구해보자면
\[\frac{\partial \mathcal{L}}{\partial H} = =\frac{\partial \mathcal{L}}{\partial z_{0}^{[2]}}W^{[2]}=W^{[2]}(\hat{y}-y)\]이다. 기억해두었다가 나중에 써먹자.
이제 다음 단계로 가서 \(\frac{\partial \mathcal{L}}{\partial W^{[1]}}, \frac{\partial \mathcal{L}}{\partial B^{[1]} }\)를 구해보자.
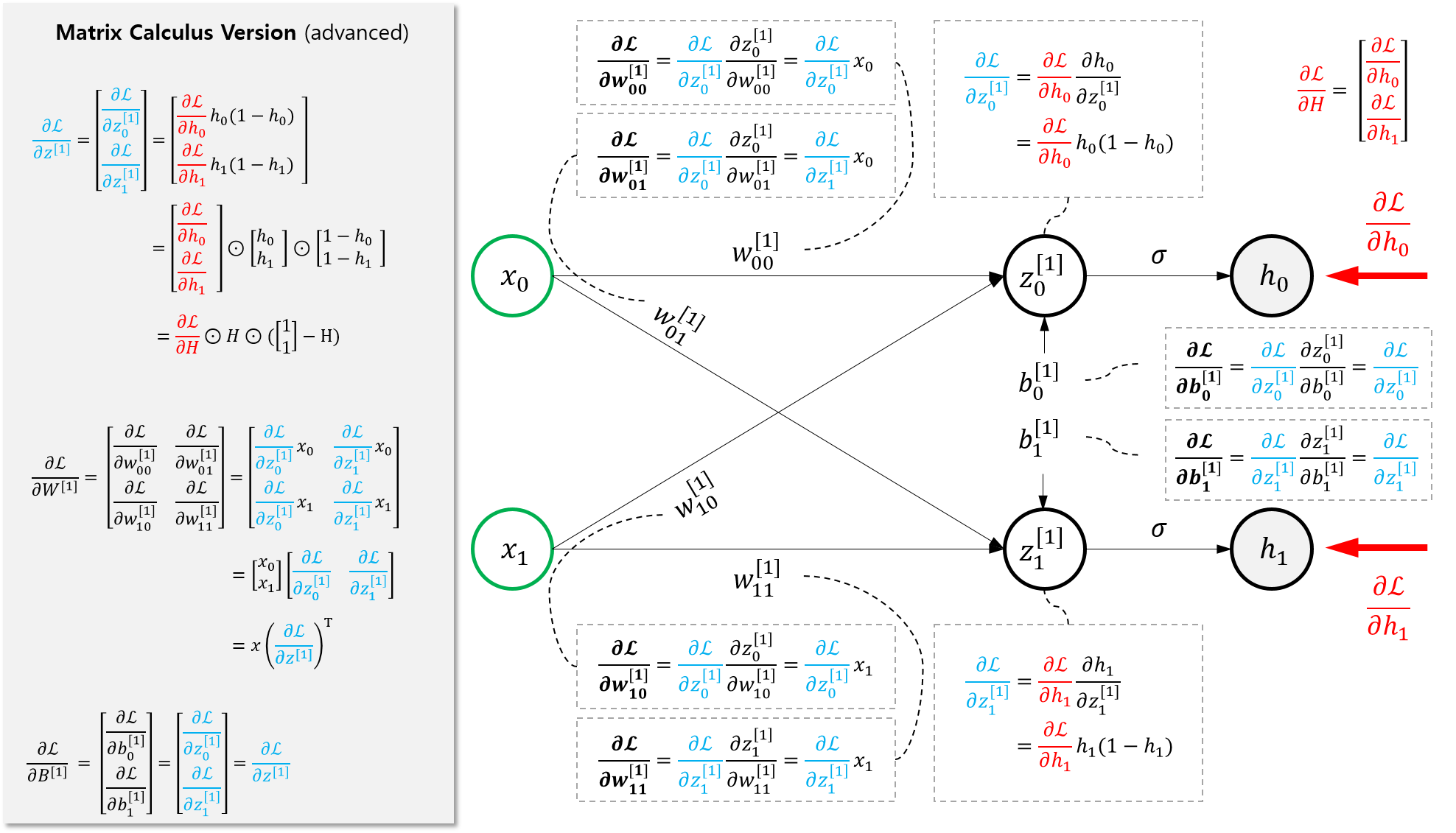
그림에서 알 수 있듯,
\[\begin{aligned} \frac{\partial \mathcal{L}}{\partial W^{[1]}} &= x (\frac{\partial \mathcal{L}}{\partial z^{[1]}})^T \\ &= x (\frac{\partial \mathcal{L}}{\partial H} \odot H \odot (\begin{bmatrix} 1 \\ 1 \end{bmatrix} -H))^T \\\\ \frac{\partial \mathcal{L}}{\partial B^{[1]}} &= \frac{\partial \mathcal{L}}{\partial z^{[1]}}\\ &=\frac{\partial \mathcal{L}}{\partial H} \odot H \odot (\begin{bmatrix} 1 \\ 1 \end{bmatrix} -H) \end{aligned}\]이다.
이제 필요한 재료는 다 모았으니, Python code로 실습을 해보자!