Logistic Regression

03 Jan 2019

Wikipedia에서 찾은 Logistic Regression의 정의는 다음과 같다.

Logistic Regression이란 ‘로지스틱 모델’의 파라미터를 예측하는 것이다.

어째 위키가 더 어려운 것 같다. 예제를 들어 더 쉽게 설명해보자.

먼저, 우리는 binary classification 문제를 풀고자 한다. binary classification문제는 관찰 가능한 벡터 \(x \in \mathbb{R}^n\)를 분석하여 이것이 특정 조건을 만족할 확률 \(0 \leq \hat{y} \leq 1\)을 예측하는 문제로 정의된다. 만약, 어떠한 \(x\)와 \(y\)의 페어 사이에 선형적인 관계 (양의 상관, 음의 상관관계)가 관찰되면, 그 문제는 로지스틱 모델을 기반으로 모델링할 수 있다. 이를 조금 더 자세하게 설명해보자.

‘로지스틱 모델’은 다음과 같은 형식을 가지고 있다.

\[\hat{y} = \sigma(w^{T}x+b)\]

이때 시그모이드라고 불리는 함수인 \(\sigma\)는 다음과 같다.

\[\sigma(z)=\frac{1}{1+e^{-z}}\]

이 시그모이드 함수의 그래프 개형은 아래와 같이 매우 예쁘게 생겼다.

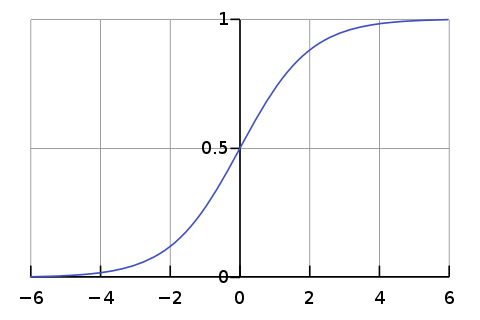
어떤점에서 예쁜가하면, 이 함수는 (0, 0.5)를 기준으로 좌우대칭이다. 또 이 함수의 특징은 input이 매우 큰 숫자가 들어오면 1을, 매우 작은 숫자가 들어오면 0을 반환한다는 점이다.

시그모이드 함수까지 설명했으니 아직 설명 안한 변수는 \(w\)와 \(b\)뿐이다. 사실 이 둘이 어떻게 정의되느냐에 따라 모델의 정확도가 매우 달라지게 된다. 비유를 하자면, \(y=ax+b\) 에서 \(a\)와 \(b\)가 바뀌면 그래프의 개형이 휙휙 바뀌지 않는가? Logistic Regrssion 모델이 파라미터를 예측한다라고 했던 위키피디아 설명은 바로 이점을 말한 것이다. 즉, 어떠한 현상을 잘 설명하는 적합한 free parameter 조합을 잘 결정해야 ‘좋은’ 모델이 된다.

그렇다면 어떤 모델이 ‘좋은’ 모델인가? 그것을 정의하기 위해 필요한 개념이 바로 cost function이다. 이 cost라는 것은 쉽게말해 에러의 합산 또는 평균이다. 내가 원하고자 하는 결과보다 얼마만큼 더 나쁜가를 수식화시킨 것이다.

조금 더 형식적으로 정의해보자. 우리가 확보한 m개의 Training Set \(T\)가 다음과 같이 생겼다고 해보자.

\[T = \{ (x^{(1)},y^{(1)}), (x^{(2)},y^{(2)}),..., (x^{(m)},y^{(m)} ) \}\]

이때 \(i\)번째 트레이닝 페어인 \((x^{(i)},y^{(i)})\)는 n차원 벡터 \(x^{(1)}\)와 0이나 1인 값 \(y^{(1)}\)로 구성되어 있다. 그렇다면 우리의 목표는 파라미터 \(w\)와 \(b\)를 잘 조정해서

\[\hat{y} = \sigma(w^{T}x+b)\approx y\]

가 되게 만드는 것이라고 할 수 있다. 위 식을 관찰하다보면 하나의 training example에 대한 error를 직관적으로 다음과 같이 정의해볼 수 있다.

\[L(\hat{y},y) =(\hat{y}-y)^2\]

즉, 차이값을 계산하기 위해 두 값의 차를 구하고, 부호의 영향력을 없애주기 위해 제곱하기! 실제로 이렇게 두고 파라미터를 최적화 시켜도, 어느정도 모델이 잘 학습되긴 한다. 그러나 이렇게 만들어진 error 함수는 convex모양이 아니기 때문에 별로 선호되지 않는다. 기술적인 내용이니, 궁금한 사람은 아래를 읽어보자.

그래프를 그렸을 때 표면이 울퉁불퉁한 함수이기 때문에 local optimization 문제(최적의 파라미터가 아니지만 국소적으로 보았을 때 최적이기 때문에 더 이상 파라미터 튜닝이 일어나지 않고 학습이 종료되는)에 빠지게 되어버린다.

대신 다음 함수를 쓴다.

\[\mathcal{L} (\hat{y},y) = -(y log{\hat{y}} + (1-y) log (1-\hat{y}))\]

위 함수는 에러를 표현하는 convex function이라는 것만 강조하고 넘어가겠다. 대신 직관적으로만 설명해보자.

• 만약 \(y=1\)일때 로지스틱 모델의 예측값이 1에 가까울수록 \(\mathcal{L}\)는 0에 수렴
• 만약 \(y=0\)일때 로지스틱 모델의 예측값이 0에 가까울수록 \(\mathcal{L}\)는 0에 수렴
• 만약 \(y=1\)일때 로지스틱 모델의 예측값이 0에 가까워지면 \(\infty\)로 발산
• 만약 \(y=0\)일때 로지스틱 모델의 예측값이 1에 가까워지면 \(\infty\)로 발산

이제 이 함수를 가지고 전체 cost function을 정의해보자.

\[J(w,b)=\frac{1}{m} \Sigma_{i}^{m} \{\mathcal{L} (\hat{y}^{(i)},y^{(i)})\}\]

이제 우리의 목적은 이 함수의 값을 최소화 시키는 파라미터 \(w, b\)를 찾는 것이다.

\[(w^*,b^*)=argmin(J(w,b))\]

어떻게 찾을 수 있을까?

Gradient Descent

우리가 중고등학교 때 배웠던 함수의 최댓값 찾기 문제는 주로 단변량 문제였다. 다변량 문제도 있긴 했으나, 많아봐야 2~3개의 변수를 다뤘다. 그러나 지금 문제의 경우 변수가 \(n+1\)개이다. 즉 미분 한번으로 함수의 최댓값을 알기 어려운 경우이다. 경사하강법 (Gradient Descent)는 이런 경우 사용할 수 있는 방법으로, global optimum 탐색을 보장하지는 못하더라도 최소한 local optimum을 찾을 수 있는 방법이다.

Gradient Descent 방법의 원리는 Wikipedia를 참조해보자. (나중에 본 포스트에서 더 자세하게 다룰 예정임)

위에서 만든 함수를 Gradient Descent 방법으로 최적화시켜보자. 그러기 위해 먼저 Loss Function \(\mathcal{L}\) 을 도식화해보자.

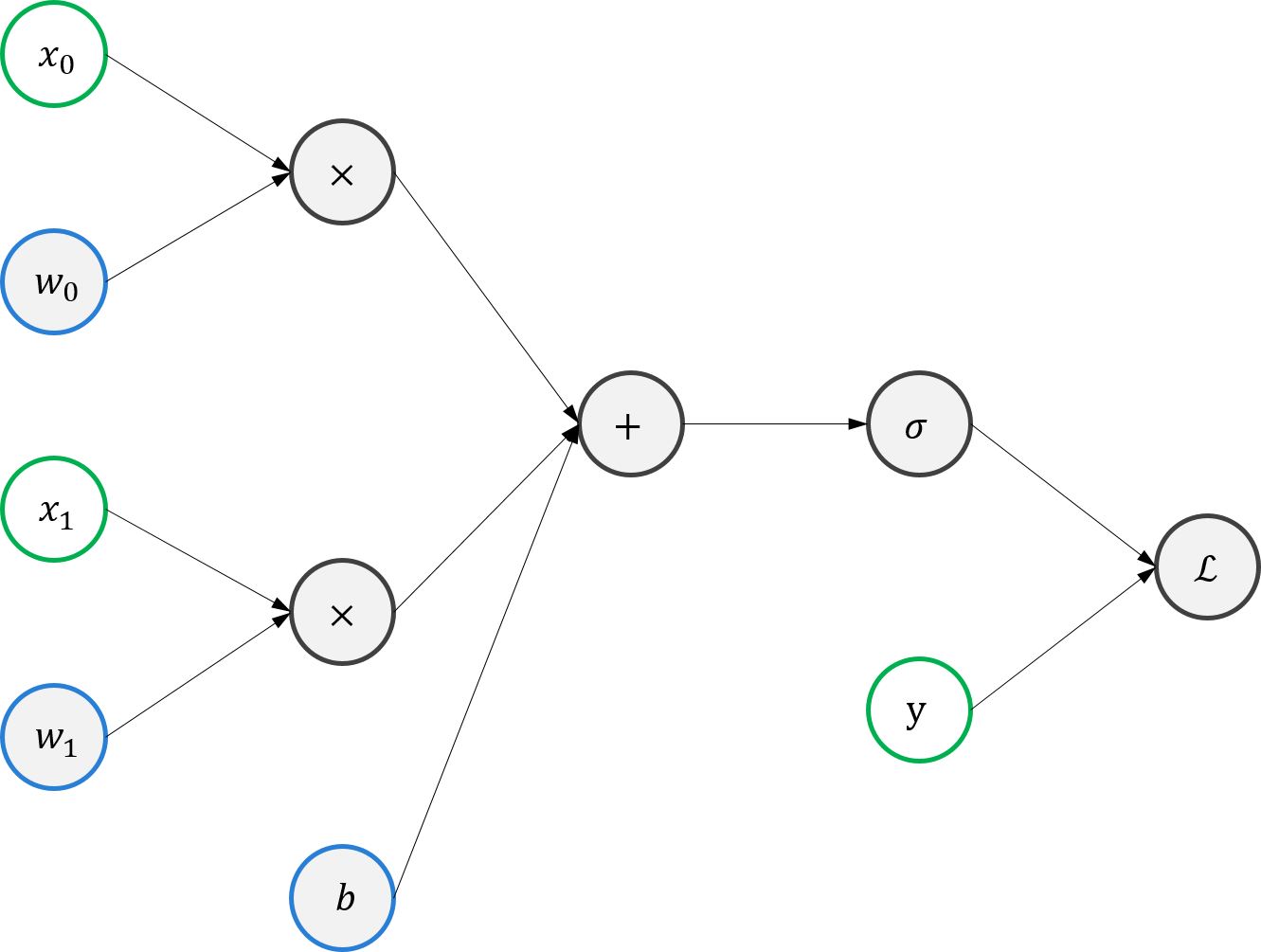
\(\mathcal{L}\)은 위 그림과 같은 과정을 통해 계산된다. 예를 들어, 우리가 가지고 있는 training set은 단 하나의 training example인 \(x=(x_{0}, x_{1}) = (0,1)\) 일 때 \(y=0\) 로만 구성되어 있다고 가정해보자. 파라미터들이 \(w=(w_{0}, w_{1}) = (0.3,0.4)\), \(b=0.5\)와 같이 초기화 되어 있었다면 \(\mathcal{L}\)은 다음과 같이 계산될 것이다.

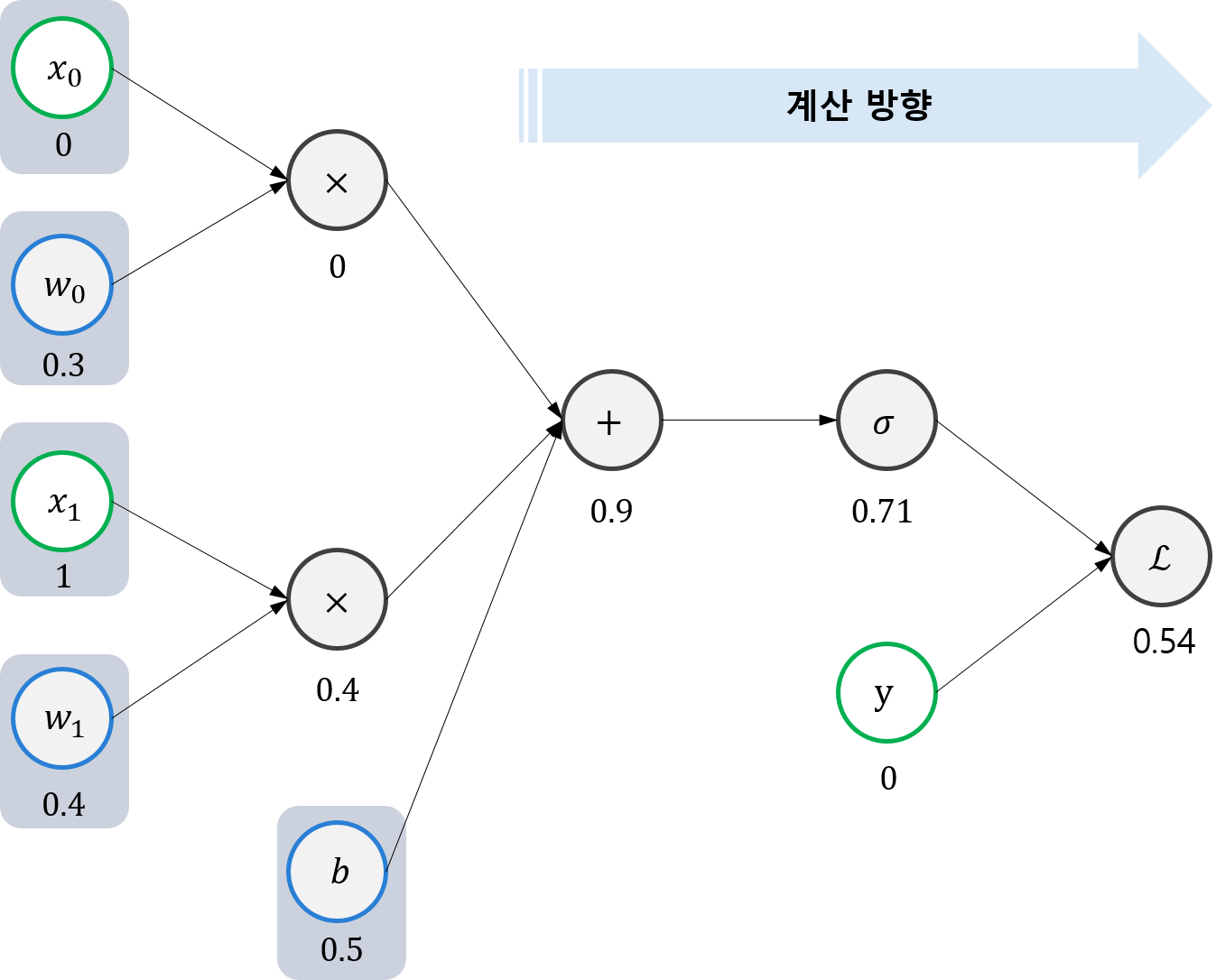
자, 보다시피 결과가 좋지 않다. 원하는 결과를 얻기 위해서는 파라미터들을 수정해주어야 할 것이다. 먼저 맨 오른쪽부터 시작해보자.

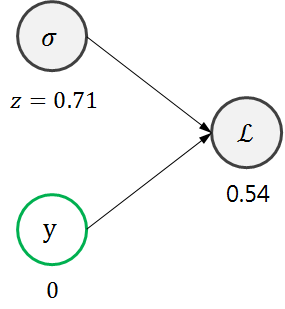
어차피 \(y\)는 우리가 바꿀 수 있는 변수가 아니다. 그러니 바꿔야하는 변수는 시그모이드 함수의 아웃풋이다. 이를 \(z\)라고 정의해보자. \(z\)는 \(\mathcal{L}\)에 어떤 영향을 미치는지 알아보기 위해 미분해보자.

\[\frac{d \mathcal{L}}{d z}=-\frac{y}{z}+\frac{1-y}{1-z}\]

위 식에 현재 \(z\)값과 \(y\)값을 대입해보면 3.46정도가 나온다. 이 말은, \(z\)값이 꽤 많이 뒤로 후퇴해야 이상적이라는 뜻이다. 맞는 말이다. 0.71은 0.5를 초과한 높은 값인데, 우리가 원하는 z값은 0에 가까운 값이니 뒤로 한참 가야한다. 이번에는 한단계 더 뒤로 가보자.

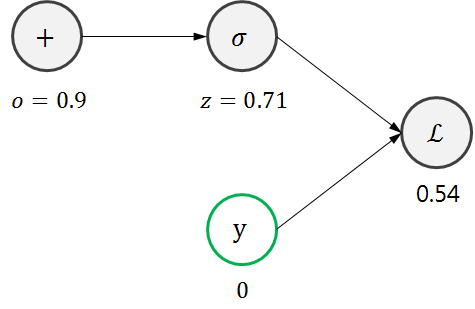
\(o\) 값, 즉 시그모이드 함수의 인풋은 어떻게 변해야할까? 이 또한 미분해보자. chain rule을 사용하여 미분할 것이다.

\[\frac{d \mathcal{L}}{d o}=\frac{d \mathcal{L}}{d z}\frac{d z}{d o}= (-\frac{y}{z}+\frac{1-y}{1-z})\frac{dz}{do}\]

chain rule을 사용했을 때 왼쪽 term은 전단계에서 이미 구한 식인니 그대로 쓰고, 이제 남은 것은 시그모이드에 대한 미분이다.

\[\frac{dz}{do}=\sigma(o)(1-\sigma(o))=z(1-z)\]

최종적으로 다음과 같은 결론 도출이 가능하다.

\[\frac{d \mathcal{L}}{d o}=\frac{d \mathcal{L}}{d z}\frac{d z}{d o}= (-\frac{y}{z}+\frac{1-y}{1-z})z(1-z)=z-y\]

식이 매우 깔끔해졌다. 위 식에 현재의 \(z\)값과 \(y\)값을 대입해보면 약 0.71이 나오는데, 이 역시 \(o\)값이 뒤로 많이 후퇴해야한다는 것을 의미한다. 이번에는 한단계 더 뒤로 가보자.

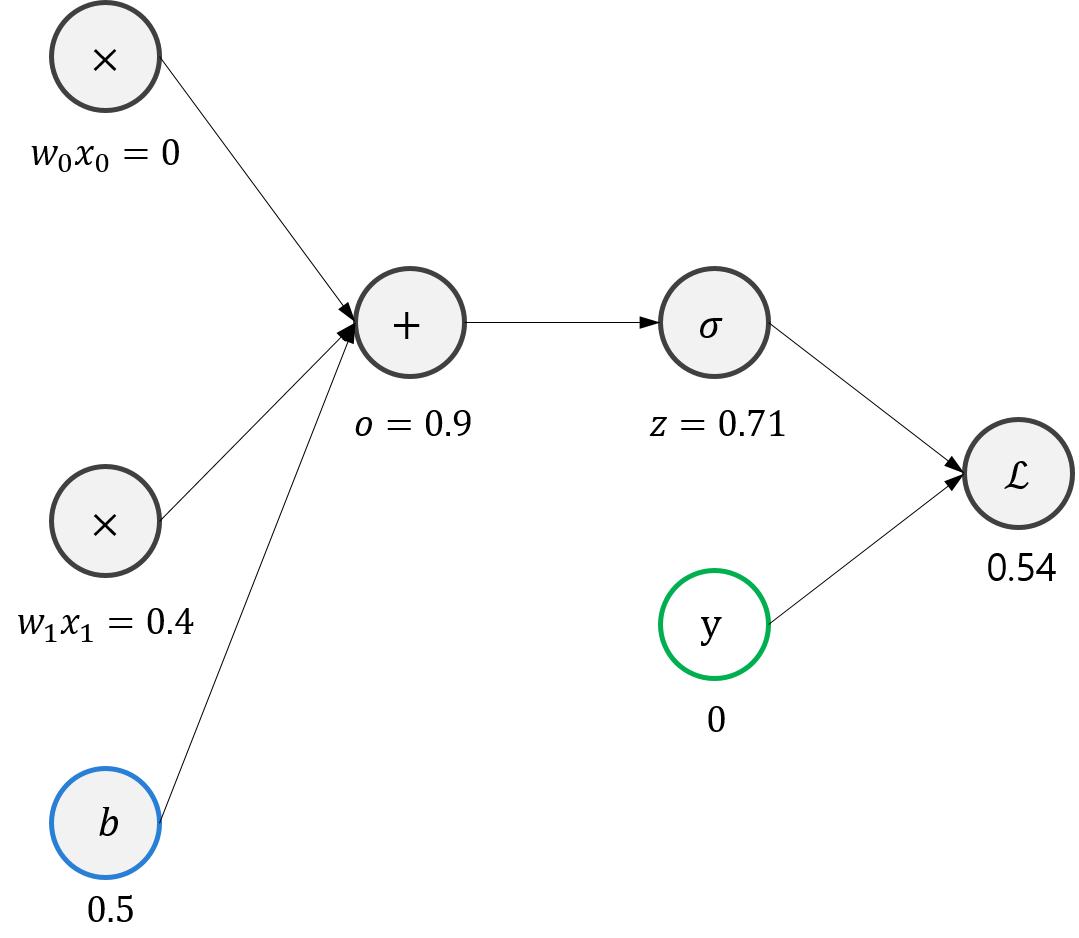
위 계산 그래프에서, \(o\)는 다음과 같이 정의된다.

\[o=w_{0}x_{0}+w_{1}x_{1}+b\]

먼저 \(w_{0}\)이 \(\mathcal{L}\)에 미치는 영향력을 보기 위해 편미분해보자.

\[\frac{\partial \mathcal{L}}{\partial w_{0}}=\frac{\partial \mathcal L}{\partial o}\frac{\partial o}{\partial w_{0}}=(z-y)x_{0}\]

같은 방식으로

\[\frac{\partial \mathcal{L}}{\partial w_{1}}=\frac{\partial \mathcal L}{\partial o}\frac{\partial o}{\partial w_{1}}=(z-y)x_{1}, \frac{\partial \mathcal{L}}{\partial b}=\frac{\partial \mathcal L}{\partial o}\frac{\partial o}{\partial b}=(z-y)\times1=z-y\]

이다.

이를 수치를 대입하여 계산해보면, \(w_{0}\)은 0만큼, \(w_{1}\)는 약 0.71만큼, \(b\)도 약 0.71만큼 비례하여 뒤로 후퇴해야한다. learning rated을 0.1로 설정해보자. 33번의 iteration을 거치면 다음과 같이 Loss 갑이 0에 가까워진다.

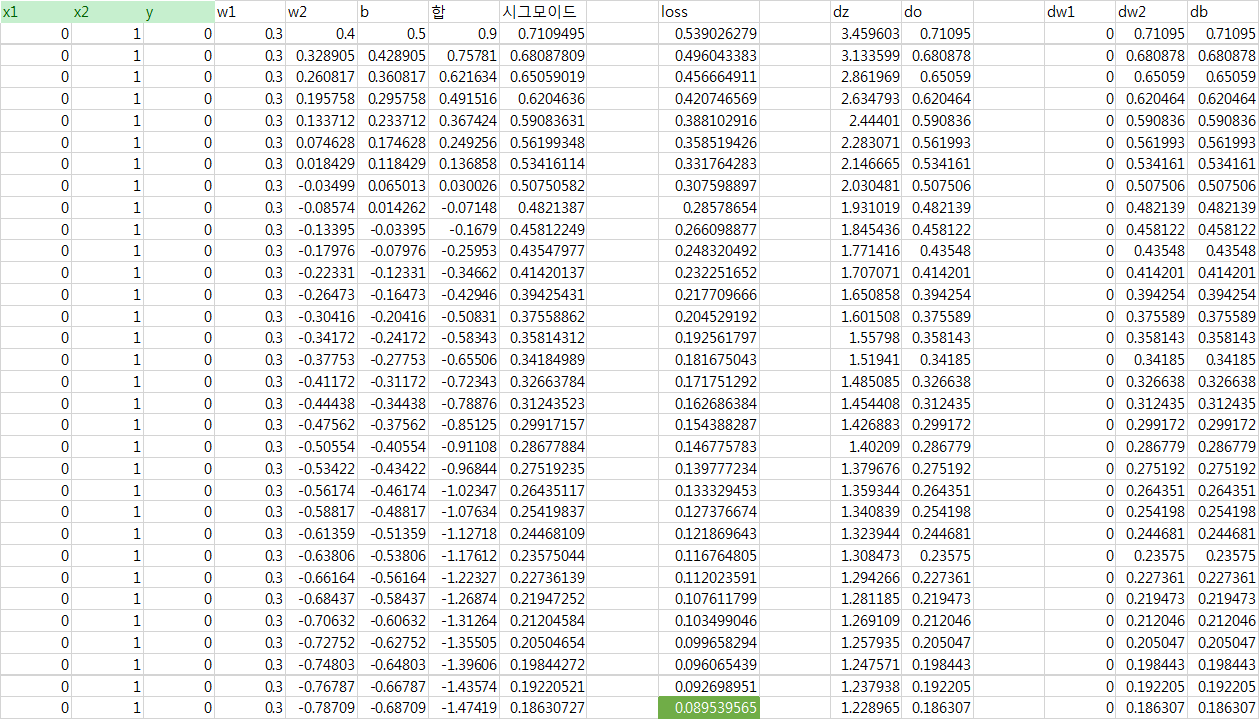
지금까지는 트레이닝 데이터가 하나인 예제를 보았다. 이제 다음과 같이 4개의 example이 있는 트레이닝 집합을 고려해보자.

\(x =(x_{0}, x_{1})\)	\(y\)
\((0,0)\)	\(0\)
\((0,1)\)	\(0\)
\((1,0)\)	\(0\)
\((1,1)\)	\(1\)

사실 이 트레이닝 데이터 집합은 And Gate (\(y=x_{0} \&\& x_{1}\))를 나타낸다. 즉 이 트레이닝 데이터 집합을 완벽하게 학습하면 And Gate역할을 하는 Logistic Regression 모델을 만들 수 있다. 이제 Python 코드로 이 트레이닝 집합을 반복적으로 학습하여 And Gate 역할을 수행하는 Logistic Regression model을 만들어보자.